どこにでもいるSEの備忘録

たぶん動くと思うからリリースしようぜ

コサイン類似度のいろんな書き方

Python

前にこんなことやってました。

www.nogawanogawa.work

コサイン類似度の計算を高速化したくなることがちょくちょくあるのですが、「ぶっちゃけどれくらいのスループットが出せるもんなの？」というのが気になったので完全に興味本位でやってみます。

コサイン類似度

定義と素朴なpythonでの実装

コサイン類似度は下記のような式になります。

\displaystyle{ cos( \vec{x}, \vec{y} ) = \frac{\vec{x} \cdot \vec{y}}{| \vec{x}| |\vec{y}|} }

これがなんの役に立つの？と考える方もいるかも知れませんが、この式は機械学習における評価関数や特徴量計算時に使用されることがあり、そういった場合には大量のコサイン類似度を計算する必要があったりして高速に計算できると実行時間自体が短くなりなにかと嬉しいことが多いという背景があります。

そんなコサイン類似度ですが、最も素朴にコサイン類似度を計算しようとするとおそらく下記のようになると思います。

import numpy as np

def cos_sim(v1, v2):
    return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))

コサイン類似度の2つの計算パターン

数式と素朴な実装は上記に表した通りなのですが、大量のコサイン類似度を計算することを考えると大きく2パターンに分けられます。

  1. 2つのベクトルの配列間ですべての組み合わせのコサイン類似度を計算
  2. 2つのベクトルの配列間で同じインデックスの組み合わせのコサイン類似度を計算

コサイン類似度計算を2分類した図

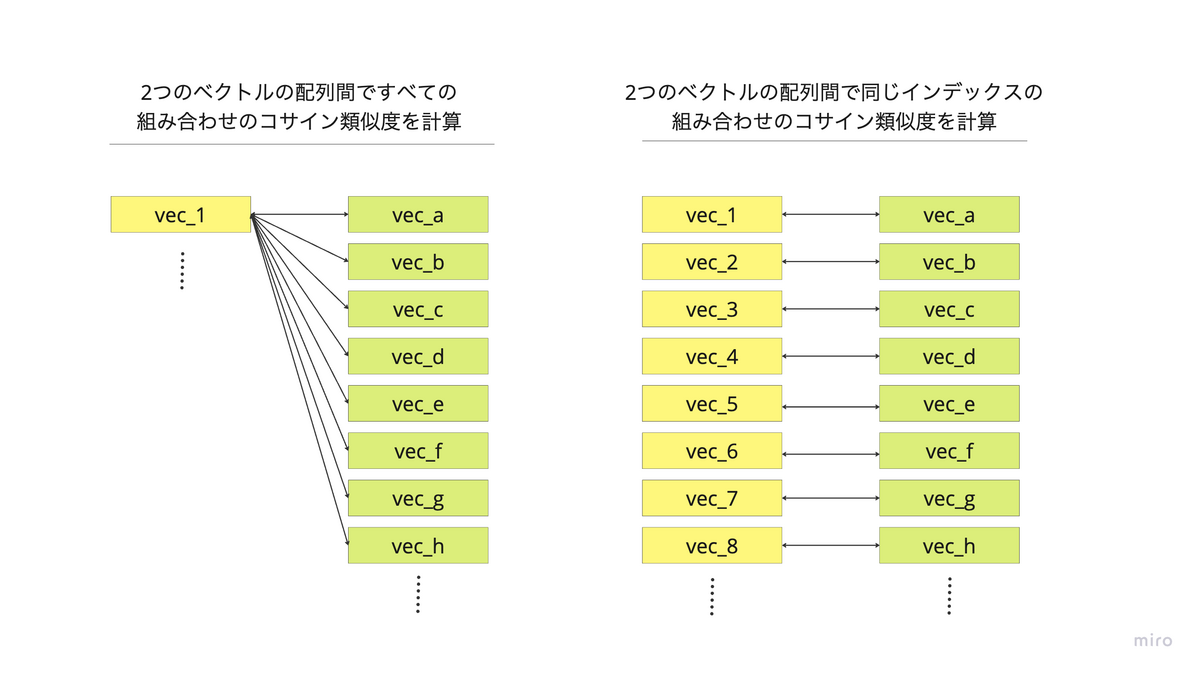
コサイン類似度を計算するライブラリの多くの場合、1.のようにすべての組み合わせに対する計算を行うことが想定されているものが多いように感じます。 一方で、2. のように同じインデックスの間で計算したいようなケースも実際には存在します。

今回はどちらも試してみて、どちらのパターンに対しても確認してみたいと思います。

諸条件

今回行う実験条件としてはこのような形になっています。

  • ベクトルはPythonのlist[list[float]]形式で保持しているものとする
    • ベクトルは200次元とする
    • ベクトルはdense (基本的にすべて0以外の実数)であるものとする
    • \vec{x}, \vec{y}のペアは5,000,000ずつ存在する
  • 何らかの高速計算用ライブラリを使用しても良い
    • ただし、型変換等にかかる時間は実行時間に含めるものとする
  • 計算環境はGoogle Colabとする（誰でも簡単に再現できるようにするため）
    • CPU: AMD EPYC 7B12 (2024年4月現在, ハイメモリを使用)

2つのベクトルの配列間ですべての組み合わせのコサイン類似度を計算

baseline

まずは素朴な実装での実行時間を計算してみようと思います。

result = [cos_sim(A[0], b) for b in B]

結果としては下記のようになりました。

CPU times: user 41.7 s, sys: 338 ms, total: 42.1 s
Wall time: 42.1 s

numpy

baselineではfor文を使用していたのですが、pythonのfor文は低速なことがわかっているので行列計算を使用することでfor文を使用しないように記述してみます。

result = np.sum(A*B, axis=1)/(norm(A, axis=1)*norm(B, axis=1))

結果としては下記のようになりました。

CPU times: user 5.31 s, sys: 5.1 s, total: 10.4 s
Wall time: 10.4 s

sklearn

sklearnにもコサイン類似度を計算する関数があるので、そちらも試してみたいと思います。 sklearnについては「2つのベクトルの配列間ですべての組み合わせのコサイン類似度を計算」するほうを想定して作られているようだったので、こちらだけ試してみます。

result = cosine_similarity(A, B)[0]

結果としては下記のようになりました。

CPU times: user 8.74 s, sys: 2.55 s, total: 11.3 s
Wall time: 9.28 s

若干ですがnumpyより高速化する結果になりました。

xlr8

その他、こちらのライブラリも高速に計算できそうだったのでやってみたいと思います。 内部実装を見る限りIntel MKL (Intel Math Kernel Library)を使用して高速化しているようです。

github.com

xlr8についても「2つのベクトルの配列間ですべての組み合わせのコサイン類似度を計算」することを想定しているようだったので、こちらだけ実験してみます。

result = cosine_similarity(A, B)[0]

こちらも結果は下記のようになりました。

CPU times: user 8.73 s, sys: 3.25 s, total: 12 s
Wall time: 9.48 s

結果としては、今回はsklearnと同程度の速度という結果になりました。

pytorch

ベクトルや行列に関する計算であれば、pytorchでも計算できそうですね。 pytorchでも計算してみます。

import torch
from torch import nn

A_torch_tensor = torch.tensor(A)
B_torch_tensor = torch.tensor(B)

cos = nn.CosineSimilarity(dim=1, eps=0)
result = cos(A_torch_tensor, B_torch_tensor)

結果としては下記のようになりました。

CPU times: user 8.27 s, sys: 22.7 s, total: 31 s
Wall time: 9.02 s

sklearnより若干ではありますが高速化する形に見えます。

jax

numpyで計算ができるということはjaxを使っても計算が可能なように思えます。 ということでjaxでもやってみたいと思います。

import jax.numpy as jnp

A_jax = jnp.array(A)
B_jax = jnp.array(B)

result = jnp.sum(A_jax * B_jax, axis=1) / (jnp.linalg.norm(A_jax, axis=1) * jnp.linalg.norm(B_jax, axis=1))

CPU times: user 5.74 s, sys: 9.5 s, total: 15.2 s
Wall time: 10.3 s

こちらですが、一見するとそれほど速くないように見えますが実際の計算部分だけに注目すると高速に計算できています。

CPU times: user 3.2 s, sys: 5.72 s, total: 8.92 s
Wall time: 3.37 s

Numba

コサイン類似度の話だとNumbaも有力でしょう。

@jit(nopython=True)
def cosine_similarity_numba(u:np.ndarray, v:np.ndarray):
    assert(u.shape[0] == v.shape[0])
    uv = 0
    uu = 0
    vv = 0
    for i in range(u.shape[0]):
        uv += u[i]*v[i]
        uu += u[i]*u[i]
        vv += v[i]*v[i]
    cos_theta = 1
    if uu!=0 and vv!=0:
        cos_theta = uv/np.sqrt(uu*vv)
    return cos_theta

result = [cosine_similarity_numba(A[0], b) for b in B]

結果としては下記のようになりました。

CPU times: user 6.64 s, sys: 231 ms, total: 6.87 s
Wall time: 7.09 s

Wall timeではNumbaが最速という結果になりました。

実行速度結果

ここまでの結果をまとめたいと思います。 結果としては下記のようになりました。

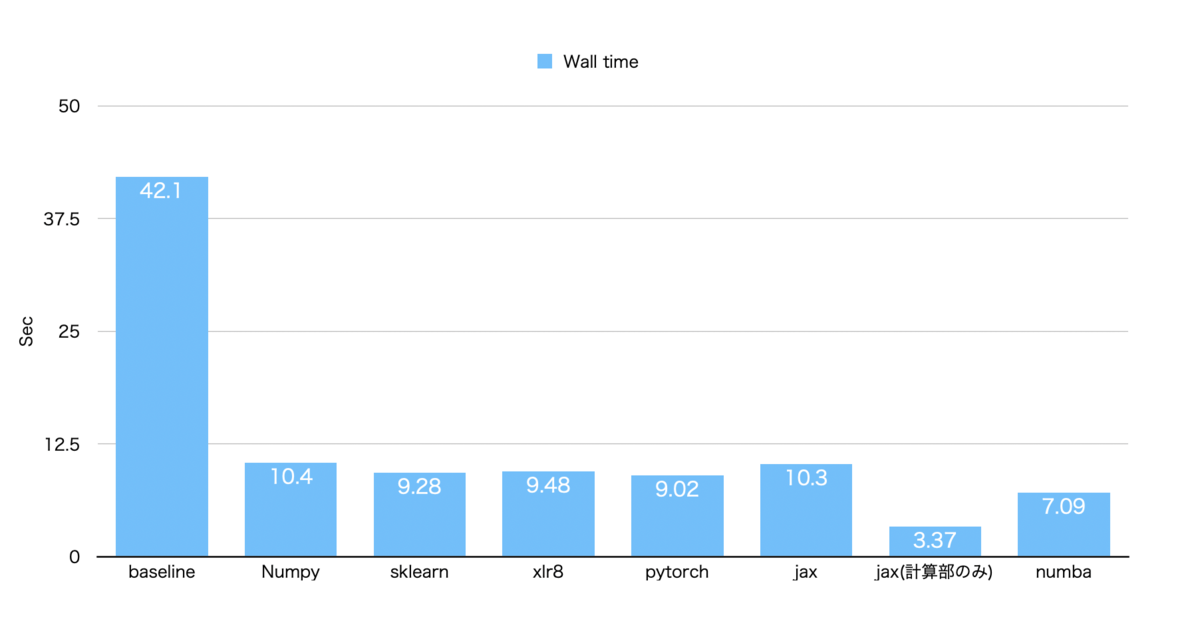
平均を取ったわけではありませんが、おおよそ傾向としては下記のようなことが言えると思います。

  • Numbaが最も高速
  • 計算部分だけならjaxが最も高速
  • その他は素朴な実装から約4倍ほど高速化

2つのベクトルの配列間で同じインデックスの組み合わせのコサイン類似度を計算

同様に2. のパターンについても実験してみます。

baseline

result = [cos_sim(a, b) for a, b in zip(A, B)]

CPU times: user 42.4 s, sys: 374 ms, total: 42.8 s
Wall time: 42.8 s

こちらについても、baselineの実装では40秒以上かかっていることになります。

numpy

result = np.sum(A*B, axis=1)/(norm(A, axis=1)*norm(B, axis=1))

CPU times: user 8.4 s, sys: 7.1 s, total: 15.5 s
Wall time: 15.3 s

やはりnumpyの行列計算を使用することで高速化しており、こちらのケースでは3倍ちかく高速化されることがわかりました。

jax

A_jax = jnp.array(A)
B_jax = jnp.array(B)

result = jnp.sum(A_jax * B_jax, axis=1) / (jnp.linalg.norm(A_jax, axis=1) * jnp.linalg.norm(B_jax, axis=1))

CPU times: user 10.1 s, sys: 16.5 s, total: 26.5 s
Wall time: 17.8 s

ただし、こちらも型変換に時間がかかっているようで、計算自体は非常に計算できていることがわかります。

CPU times: user 5.04 s, sys: 8.56 s, total: 13.6 s
Wall time: 5.19 s

計算部分だけ見ると今回もjaxが最速という結果になりました。

Numba

改めてNumbaで計算してみます。

result = [cosine_similarity_numba(a, b) for a, b in zip(A, B)]

CPU times: user 5.46 s, sys: 80.2 ms, total: 5.54 s
Wall time: 5.56 s

こちらもNumbaを使うのが最も高速という結果になりました。

実行速度結果

「2つのベクトルの配列間で同じインデックスの組み合わせのコサイン類似度を計算」する方について、今回の結果は下記のようになりました。

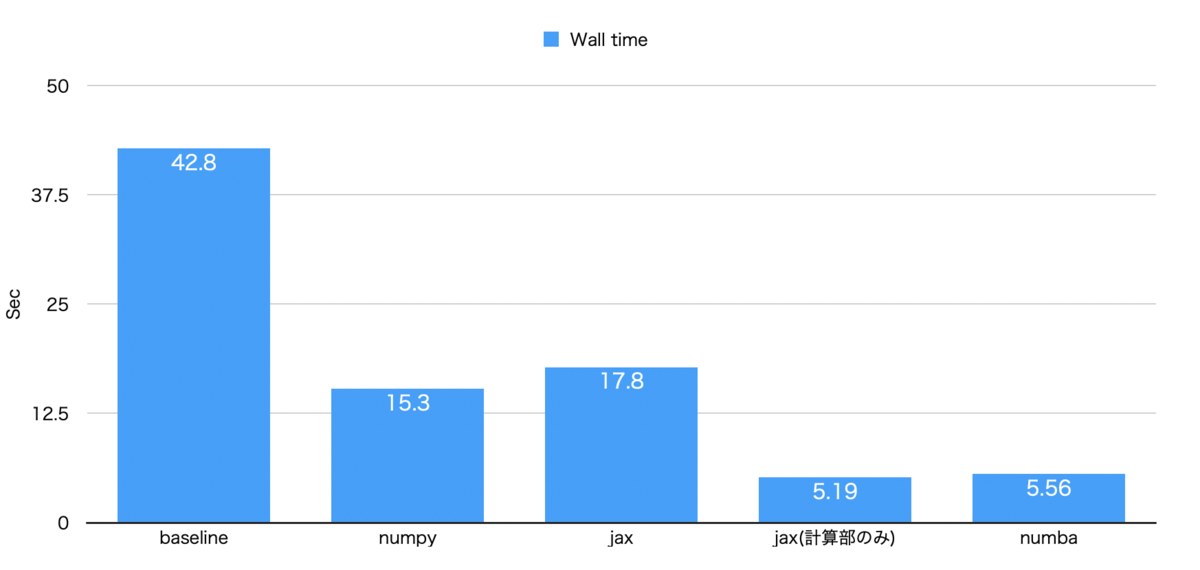
こちらも先ほど同様、傾向としては下記のようなことが言えると思います。

  • Numbaが最も高速
  • 計算部分だけならjaxが最も高速
  • その他は素朴な実装から約3倍ほど高速化

使用したコード

今回使用したソースコードはこちらにあるので、ご自由にご利用ください。

参考文献

感想

CPU上で自分が思いつく限りのコサイン類似度計算を一通りやってみました。 結果としては

  1. 総合的にはNumbaが高速
  2. jaxを使用していて型変換が不要な状況であれば、計算自体はjaxが最も高速

という結果になりました。 numpyだけを使用してもそこそこ高速ではある点はちょっと意外でした。

世の中の高速化に関する最適化手法を全て試すのは無理なので、もし「こっちのほうが速い」という知見があればこっそり教えていただければと思います！

ランキング参加中
Python

ランキング参加中
プログラミング